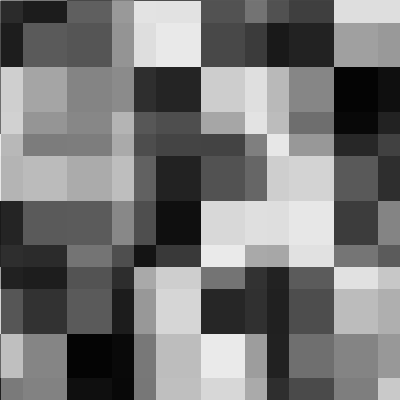Rendering surfaces
Scope
I want to present an idea of rendering 3D surfaces derived from vector fields. It’s one of the algorithms I used in my math art folds2d project.
What do we need
We will rely on methods implemented in clojure2d and fastmath libraries.
Let’s require the following namespaces:
clojure2d.core,c2d- 2D drawingclojure2d.color,c- colors, palettes and gradientsclojure2d.pixels,p- pixel manipulation and renderingclojure2d.extra.utils,utls- gradient viewerfastmath.core,m- primitive mathfastmath.vectors,v- primitive 2D, 3D and 4D vectorsfastmath.random,r- randomness and noisefastmath.fields,f- vector fields
(require '[clojure2d.core :as c2d]
'[clojure2d.color :as c]
'[clojure2d.pixels :as p]
'[clojure2d.extra.utils :as utls]
'[fastmath.core :as m]
'[fastmath.vector :as v]
'[fastmath.random :as r]
'[fastmath.fields :as f])(import [fastmath.vector Vec2 Vec3])fastmath.vector.Vec33D to 2D projection
Let’s start with very basic 3D rendering of the scene. We won’t rely on the ray tracing algorithm but something opposite. The assumption is that every point of given surface is a light source and we want to capture these light by the camera sensor. No shadows, reflections, external light sources etc. We need only depth of the field and perspective to achieve perception of the 3D scene.
For given sample surface point \(\vec{v}=(x,y,z)\) we can define a perspective projection as \(\vec{v_p}=P(\vec{v})=(\frac{x}{d},\frac{y}{d})\), where \(d\) is a distance between camera and point along the \(z\) axis.
Camera has fixed position \((0,0,c_z)\) and faces towards the origin.
Depth of the field is created by bluring points which are not in the focus point. Radius of the blur is calculated by the formula \(r_{m,e}(d)=m\lvert f-d\rvert^e\). \(m\) and \(e\) define how much blur to apply. Blur is achieved by shifting projected point by a random vector sampled from a disc of radius r. To make it we will use a r/ball-random function which returns a uniform sample from an unit disc.
(r/ball-random 2)[0.08632393742033892 0.15872471978238484]The following creator makes projecting function which returns blurred 2D point and a distance to the camera as z. Distance will be later used to simulate light intensity, since further points should be dimmed.
In this presentation we assume that camera is always at \(z=-7\) and focus is always at \(z=0\). Also, \(m=0.005\) and \(e=0.5\).
(defn ->perspective-projection
[^double camera-z ^double m ^double e]
(fn [^Vec3 v]
(let [d (m/abs (m/- (.z v) camera-z))
xy (v/div (v/vec2 (.x v) (.y v)) d)
r (m/* m (m/pow (m/abs (m/+ camera-z d)) e))
blur (v/mult (r/ball-random 2) r)]
(v/vec3 (v/add xy blur) d))))(def projection (->perspective-projection -7.0 0.005 0.5))(projection (v/vec3 2 2 -5))[1.0076331653805384 0.9935635017295776 2.0]Rectangles
Let’s start with simple parallel and slightly rotated rectangles. Rectangles will have \(y=-2\) or \(y=2\) and \(x=z=(-6,6)\). The following function will uniformly sample points from them.
(defn sample-rectangles []
(let [x (r/drand -6.0 6.0)
z (r/drand -6.0 6.0)
y (r/randval -2.0 2.0)]
(v/vec3 x y z)))(repeatedly 5 sample-rectangles)([-4.79027732606705 2.0 -0.7336607376515047]
[2.3645695880232704 -2.0 4.242625832114182]
[4.177835505993841 -2.0 2.65627283903288]
[1.6135054988134492 -2.0 3.9401821515375026]
[5.590408941654648 -2.0 3.810360944362383])And let’s project some points to 2D
(repeatedly 5 (comp projection sample-rectangles))([-0.4102703250318156 0.1528191423365527 12.969724166890707]
[0.6429413250231744 0.6148715547778631 3.2816315207454543]
[-1.8703561122545815 -0.7266509012063082 2.726082611852714]
[0.2892828655388859 -0.396836851048834 5.054893722831816]
[-0.27796822151169714 0.17208273847003244 11.45290369092236])Ok! Now let’s see how it renders. camera->screen function converts a camera coordinates to a screen (image) coordinates.
(defn camera->screen
[^Vec2 vp ^double screen-size]
(v/vec2 (m/norm (.x vp) -3.0 3.0 0.0 screen-size)
(m/norm (.y vp) -3.0 3.0 0.0 screen-size)))v/rorate is a function which rotates given 3D vector along x,y and z axes. We rotate sampled pixel before projecting it to a camera.
(c2d/with-canvas [canv (c2d/canvas 400 400)]
(c2d/set-background canv :black)
(c2d/set-color canv :white 20)
(doseq [v (repeatedly 200000 sample-rectangles)]
(let [vrot (v/rotate v 0.1 0.1 0.2)
vp (projection vrot)
xy (camera->screen (v/vec2 vp) 400)]
(c2d/point canv xy)))
(c2d/to-image canv))As we can see, further points are brighter and too saturated. We need to lower alpha for further points according to the inverse-square law.
(c2d/with-canvas [canv (c2d/canvas 400 400)]
(c2d/set-background canv :black)
(doseq [v (repeatedly 1000000 sample-rectangles)]
(let [vrot (v/rotate v 0.1 0.1 0.2)
^Vec3 vp (projection vrot)
xy (camera->screen (v/vec2 vp) 400)
d (.z vp)
alpha (m// 150.0 (m/sq d))]
(c2d/set-color canv :white alpha)
(c2d/point canv xy)))
(c2d/to-image canv))When the number of samples is big enough we can see some artifacts caused by additive method of alpha blending used by Java2D rendering engine. We have to switch to other rendering method.
Log-density rendering
Log-density rendering is a method based on counting amount of light (separate for R, G and B channels, weighted by an alpha value) incoming to a given pixel, similarly to a digital camera sensor. After all samples are collected, data are normalized and logarithm is applied to boost darker areas (this is a default behaviour and can be turned off) . Then everything is converted back to a RGB values.
Additionally we can apply smoothing (reconstruction) kernel for anti-aliasing. It will be used in final render.
(let [canv (p/renderer 400 400)]
(doseq [v (repeatedly 1000000 sample-rectangles)]
(let [vrot (v/rotate v 0.1 0.1 0.2)
^Vec3 vp (projection vrot)
^Vec2 xy (camera->screen (v/vec2 vp) 400)
d (.z vp)
alpha (m/constrain (m// 100.0 (m/sq d)) 0.0 255.0)]
(p/set-color! canv (.x xy) (.y xy) (c/set-alpha :white alpha))))
(-> canv
(p/to-pixels)
(c2d/to-image)))Note: p/to-pixels allows some postprocessing like adjusting contrast, brightness, saturation or applying gamma correction. We will use it later.
Surfaces
Before we start to construct surfaces, let’s add a little bit of distortion to our planes. For that we are going to use noise function.
Noise
First we’ll visualize already defined noise in fastmath.random namespace. Noise returns a value between 0.0 and 1.0.
(defn draw-2d-noise
[noise]
(c2d/with-canvas [canv (c2d/canvas 400 400)]
(doseq [x (range 400)
y (range 400)]
(let [xx (m/norm x 0 400 -3 3) ;; screen to f domain transformation
yy (m/norm y 0 400 -3 3)
v (double (noise xx yy))]
(c2d/set-color canv (c/gray (m/* 255.0 v))) ;; black for 0.0, white for 1.0
(c2d/point canv x y)))
(c2d/to-image canv)))(kind/table
[["Value noise" "Perlin noise" "Open simplex noise"]
[(draw-2d-noise r/vnoise)
(draw-2d-noise r/noise)
(draw-2d-noise r/simplex)]])To create distortion we need to build a 3D vector constructed from noise function for given point.
(defn noise-distortion
[noise ^Vec3 vin]
(let [nx (noise (.x vin) (.y vin) (.z vin))
ny (noise (.y vin) (.z vin) (m/+ 0.123 (.x vin)))
nz (noise (.z vin) (.x vin) (m/+ 0.654 (.y vin)))]
(v/vec3 nx ny nz)))(noise-distortion r/vnoise (v/vec3 0.2 0.3 0.4))[0.381878995334099 0.4419369949064613 0.4309128917573337]Now we can apply distortion to our planes. We add distortion vector before rotation.
(let [canv (p/renderer 400 400)]
(doseq [v (repeatedly 1000000 sample-rectangles)]
(let [vn (v/add v (v/mult (noise-distortion r/vnoise v) 0.25))
vrot (v/rotate vn 0.1 0.1 0.2)
^Vec3 vp (projection vrot)
^Vec2 xy (camera->screen (v/vec2 vp) 400)
d (.z vp)
alpha (m/constrain (m// 100.0 (m/sq d)) 0.0 255.0)]
(p/set-color! canv (.x xy) (.y xy) (c/set-alpha :white alpha))))
(-> canv
(p/to-pixels)
(c2d/to-image)))My original idea used less smooth noise function. fastmath allows defining own noise functions from given specification.
We need FBM value noise without interpolation, we need just 3-4 octaves included. r/random-noise-fn will create such function with some random seed. We want to set lacunarity to not integer value to make layers which are not aligned.
(defn random-noise
[octaves]
(r/random-noise-fn {:noise-type :value
:warp-scale 0.0
:gain 0.5
:lacunarity 1.5
:interpolation :none
:generator :fbm
:octaves octaves}))(kind/table
[["Single layer" "Two layers" "Four layers"]
[(draw-2d-noise (random-noise 1))
(draw-2d-noise (random-noise 2))
(draw-2d-noise (random-noise 4))]])Final effect makes quite blocky structure like Arrakeen city or Death Star surface.
(let [noise (random-noise 4)
canv (p/renderer 400 400)]
(doseq [v (repeatedly 1000000 sample-rectangles)]
(let [vn (v/add v (v/mult (noise-distortion noise v) 0.25))
vrot (v/rotate vn 0.1 0.1 0.2)
^Vec3 vp (projection vrot)
^Vec2 xy (camera->screen (v/vec2 vp) 400)
d (.z vp)
alpha (m/constrain (m// 100.0 (m/sq d)) 0.0 255.0)]
(p/set-color! canv (.x xy) (.y xy) (c/set-alpha :white alpha))))
(-> canv
(p/to-pixels)
(c2d/to-image)))Vector fields
A vector field in our case is just a 2D to 2D function. It shouldn’t be smooth, differentiable, it can be even random. For example \(F(\vec{v})=(\sin(\vec{v}(x)),\sin(\vec{v}(y)))\) is a valid vector field, we call it sinusoidal.
(defn sinusoidal [v] (v/sin v))(sinusoidal (v/vec2 1 2))[0.8414709848078964 0.9092974268256818]Let’s illustrate how given vector field transforms a square area.
(defn draw-field
([field] (draw-field field 4.0))
([field ^double scale]
(let [scale- (m/- scale)]
(c2d/with-canvas [c (c2d/canvas 400 400)]
(c2d/set-background c :black)
(c2d/set-color c (c/gray 200 50))
(dotimes [_ 250000]
(let [x (r/drand -4.0 4.0)
y (r/drand -4.0 4.0)
vin (v/vec2 x y)
^Vec2 vout (field vin)
xout (m/norm (.x vout) scale- scale 0.0 400.0)
yout (m/norm (.y vout) scale- scale 0.0 400.0)]
(c2d/point c xout yout)))
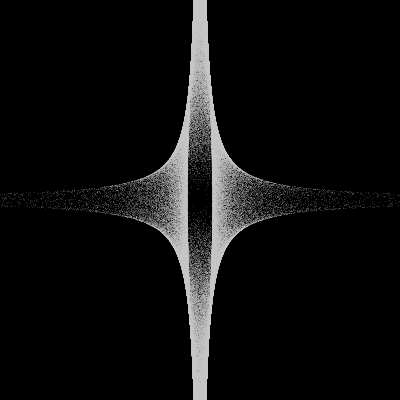
(c2d/to-image c)))))(draw-field sinusoidal 1.1)Another one creates diamond-like shape, \(F(\vec{v})=(\frac{\vec{v}(x)}{\Vert{\vec{v}}\Vert}\cos(\Vert{\vec{v}}\Vert), \frac{\vec{v}(y)}{\Vert{\vec{v}}\Vert}\sin(\Vert{\vec{v}}\Vert))\)
(defn diamond [^Vec2 v]
(let [length (v/mag v)
sina (m// (.x v) length)
cosa (m// (.y v) length)
sinr (m/sin length)
cosr (m/cos length)]
(v/vec2 (m/* sina cosr)
(m/* cosa sinr))))(draw-field diamond 1.1)Finally our surfaces will be build the following way (here is the 2D case):
- for given \(\vec{v}=(x,y)\) sampled from a square \(S=(-3,3)\times(-3,3)\)
- calculate fields values \(\vec{v_x}=F_1(\vec{v})\) and \(\vec{v_y}=F_2(\vec{v})\)
- calculate angles \(a_x=\operatorname{atan2}(\vec{v_x}(y), \vec{v_x}(x))\), the same for \(a_y\)
- construct \(\vec{v_{out}}=(a_x, a_y)\) and plot it.
The same procedure applies to 3D case, the only addition is third vector field, \(\vec{v_z}\) and \(a_z\).
(defn draw-angles-2d
[field1 field2]
(c2d/with-canvas [c (c2d/canvas 400 400)]
(c2d/set-background c :black)
(c2d/set-color c (c/gray 200 50))
(dotimes [_ 250000]
(let [x (r/drand -4.0 4.0)
y (r/drand -4.0 4.0)
vin (v/vec2 x y)
vx (field1 vin)
vy (field2 vin)
ax (v/heading vx)
ay (v/heading vy)
xout (m/norm ax -3.5 3.5 0.0 400.0)
yout (m/norm ay -3.5 3.5 0.0 400.0)]
(c2d/point c xout yout)))
(c2d/to-image c)))(draw-angles-2d sinusoidal diamond)fastmath.fields contains almost 400 already defined vector fields or families of fields (parametrized fields). Many of them are used as variations in fractal flame algorithm.
(count f/fields-list)386f/field creates defined vector field by name and optional scaling factor (default 1.0) and parameters (if available, randomly selected by default).
(kind/table
[["Hyperbolic field" "Rays field" "Angles 2D"]
[(draw-field (f/field :hyperbolic))
(draw-field (f/field :rays))
(draw-angles-2d (f/field :hyperbolic) (f/field :rays))]])The following creator builds a sampler for our surface from given vector fields.
(defn ->fields-sampler
[field1 field2 field3]
(fn []
(let [x (r/drand -4.0 4.0)
y (r/drand -4.0 4.0)
v (v/vec2 x y)
vx (field1 v)
vy (field2 v)
vz (field3 v)]
[vx vy vz])))Define blocky noise as a global var.
(def noise (random-noise 4))And finally we render surface. We add gaussian smoothing kernel and bump brightness a little bit.
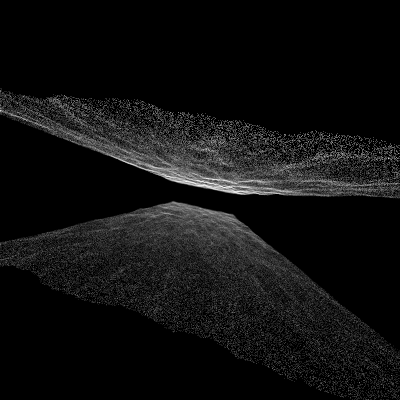
(let [sampler (->fields-sampler
(f/field :diamond)
(f/field :rays)
(f/field :hyperbolic))
canv (p/renderer 400 400 :gaussian)]
(doseq [[vx vy vz] (repeatedly 1000000 sampler)]
(let [ax (v/heading vx)
ay (v/heading vy)
az (v/heading vz)
v (v/vec3 ax ay az)
vn (-> (noise-distortion noise v)
(v/mult 0.25)
(v/add v)
(v/mult 2))
vrot (v/rotate vn 0.2 0.2 0.2)
^Vec3 vp (projection vrot)
^Vec2 xy (camera->screen (v/vec2 vp) 400)
d (.z vp)
alpha (m/constrain (m// 100.0 (m/sq d)) 0.0 255.0)]
(p/set-color! canv (.x xy) (.y xy) (c/set-alpha :white alpha))))
(-> canv
(p/to-pixels {:brightness 1.5})
(c2d/to-image)))Color
The last element is a color for the shape. We can use magnitudes as a color selector. We need to convert length of the vectors to a value from 0.0 to 1.0 and use this value as selector from the following gradient.
(c2d/resize (utls/gradient->image (c/palette 18)) 600 200)List of possible palettes is here.
Now we are ready to render final image. Saturation, gamma and brightness are boosted. Contrast is sligthly lowered. Also, gaussian smoothing kernel is used.
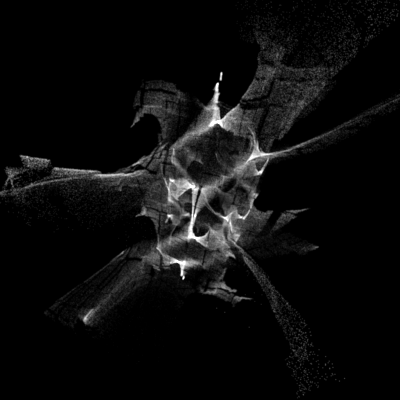
(defn draw-angles-3d
[{:keys [field1 field2 field3 ^long sample-size ^long palette-id ^long screen-size]
:or {sample-size 1000000 palette-id 18 screen-size 400}}]
(let [sampler (->fields-sampler field1 field2 field3)
canv (p/renderer screen-size screen-size :gaussian)
gradient (c/gradient (c/palette palette-id))]
(doseq [[vx vy vz] (repeatedly sample-size sampler)]
(let [ax (v/heading vx)
ay (v/heading vy)
az (v/heading vz)
v (v/vec3 ax ay az)
mx (v/mag vx)
my (v/mag vy)
mz (v/mag vz)
color (gradient (m/sq (m/sin (m/+ mx my mz))))
vn (-> (noise-distortion noise v)
(v/mult 0.25) ;; scale noise
(v/add v) ;; distort
(v/mult 2)) ;; magnify object
vrot (v/rotate vn 0.2 0.2 0.2)
^Vec3 vp (projection vrot)
^Vec2 xy (camera->screen (v/vec2 vp) screen-size)
d (.z vp)
alpha (m/constrain (m// 100.0 (m/sq d)) 0.0 255.0)]
(p/set-color! canv (.x xy) (.y xy) (c/set-alpha color alpha))))
(-> canv
(p/to-pixels {:brightness 2 :saturation 1.5 :contrast 0.9 :gamma-color 1.5 :gamma-alpha 1.2})
(c2d/to-image))))(comment (-> (draw-angles-3d {:field1 (f/field :diamond) :field2 (f/field :rays) :field3 (f/field :hyperbolic)
:sample-size 50000000 :screen-size 1000})
(c2d/save "src/generative_art/surfaces/final_full_size.jpg"))
(-> (draw-angles-3d {:field1 (f/field :diamond) :field2 (f/field :rays) :field3 (f/field :hyperbolic)})
(c2d/save "src/generative_art/surfaces/final_small.jpg")))